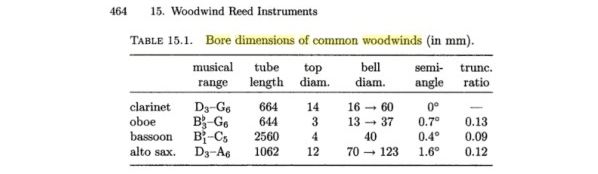
We know from Benade that the frequency = speed of sound divided by the wavelength for which the formula is
f = C/W where
f is the frequency C is the speed of sound in meters per second and W represents the wavelength of the sound in meters. On the saxophone
W = 2L where L is the physical length of the sounding tube.
The
natural resonant frequency of an alto saxophone in good repair can be found by fingering low Bb on the instrument and neck without its mouthpiece, and by "popping" one of the right hand keys. One can hear a pitch clearly by putting the end of the neck up to one's ear like a stethoscope. This pitch can also be measured by placing the opening of the neck against the speaker/microphone of a tuner.
On a
Selmer SBA alto the
natural resonant frequency was measured at
E3 Concert 45 cents sharp.
At C = 345m/sec
the frequency of E3 45c sharp is 169.22hz.
Using the formula W = C/
f the wave length for the 45c sharp E3 is 2.0388m or 203.88cm.
For the saxophone W = 2L, so the
"acoustic" length of the saxophone "tube" is 203.88cm/2 or
101.94cm.
[This is in close agreement with the measured physical dimensions of 102.1cm given in the attachment above.]
The lowest played note on an alto saxophone is written Bb or
Db3 concert with a frequency of 138.59hz and wavelength of 248.93cm
Since W = 2L, the
"acoustic length" of a saxophone playing its lowest note is 248.93cm/2 or
124.47cm.
- 124.47cm Db3 concert
- 101.94cm E3 concert 45c sharp
- 22.53cm difference
If we assume 22.53cm to be the length of the missing cone, then it is possible to calculate the slope that would produce that length given the small opening of the neck. Using Ferron's* formula slope = 28.65(d - 0)/l where 28.65 is the multiplier to convert the slope to degrees, d is the diameter of the small opening of the neck, 0 is the diameter of the point of the cone and l is the length. The calculation would be as follows.
slope = 28.65(12.6mm - 0)/225.3mm = 1.60°
Adding the measured length of the neck including the tenon 19.7cm to the calculated length of the missing cone 22.53cm gives 42.23cm
Since the wavelength of the pitch produced is 2L, the result is 84.46cm. The frequency of
a note with this wavelength is 408.48hz.
- 415.3hz Ab3
- 408.5hz pitch of neck + missing cone
- 6.8hz difference 1hz = 4.3c 6.8hz = 29c so the theoretical pitch of the neck plus missing cone is Ab3 29 cents flat.
In the next installment this "calculated taper" to find the missing cone will be compared to the measured tapers on the instrument and there will be a demonstration of how a measurement being off by just .1mm can have a dramatic effect upon the missing cone calculations using Ferron's* methodology.
*The Saxophone is my Voice" by Ernest Ferron.